Antes nos desviamos considerablemente de nuestro objetivo principal: estudiar cómo podría responderse la pregunta ¿qué ecuación se puede resolver? Primero, la restringimos a las ecuaciones algebraicas. Y, hasta ahora, sólo llegamos a la conclusión de que con los números complejos podemos resolver cualquier ecuación cuadrática (13) con parámetros a, b y c reales. No obstante, vimos que podemos sacar la raíz cuadrada de cualquier número complejo, lo cual nos podría dar la idea de cuestionar si sería posible resolver (13), aun cuando los parámetros a, b, c sean números complejos, como en:
En efecto, lo anterior es cierto y se usa exactamente la misma fórmula (14) que antes. La razón se debe a que esta fórmula se deriva de manera algebraica sin hacer ninguna suposición, excepto que a ≠0. Consideremos esta deducción y pensemos que a, b, c son números complejos. Primero, se divide la ecuación entre a:
Luego, se suma el término 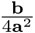 en ambos lados y se observa que
en ambos lados y se observa que 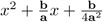 es un cuadrado perfecto:
es un cuadrado perfecto:
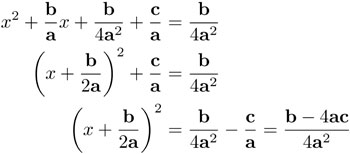
En la última fila, se restó el término 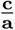 en ambos lados. Ahora se puede sacar la raíz. Recordemos aquí que ello siempre se puede, dado que
en ambos lados. Ahora se puede sacar la raíz. Recordemos aquí que ello siempre se puede, dado que  es un número complejo y, por lo tanto, siempre hay dos soluciones, salvo cuando
es un número complejo y, por lo tanto, siempre hay dos soluciones, salvo cuando 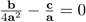 .
.
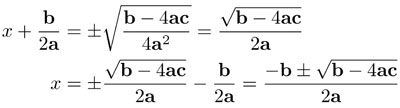
De nuevo obtuvimos la fórmula de solución (14) y de nada importó que los coeficientes a,b y c sean complejos.